Цель расчета: выбор элементов воздушных линий с прочностью, которая обеспечивает их безаварийную эксплуатацию при механических нагрузках, не превышающих нагрузок, имеющих место при самом неблагоприятном сочетании расчетных условий.
Исходные данные
Расчет выполняется для строительства воздушной линии 0.4кВ с самонесущим изолированным проводом для опор на базе железобетонных стоек.
Район строительства ВЛИ-0.4кВ: Алматинская обл., г.Талгар.
Климатические условия района проектируемой ВЛИ:
– Абсолютная минимальная температура воздуха: t_= –43°C (СНиП РК 2.04-01-2010 «Строительная климатология», табл. А.1);
– Абсолютная максимальная температура воздуха: t+=43°C (СНиП РК 2.04-01-2010 «Строительная климатология», табл. А.2);
– Средняя годовая температура воздуха: t_ср=8.9°C (СН РК 2.04-21-2004* «Энергопотребление и тепловая защита гражданских зданий», табл. 3.5; СНиП РК 2.04-01-2010 «Строительная климатология», п.4.5г);
– Район по толщине стенки гололеда: III, что соответствует нормативной толщине стенки гололеда 15мм с повторяемостью 1 раз в 10 лет (ПУЭ РК 2003г., п.2.4.11., табл.2.5.3.);
– Район по давлению ветра: II, что соответствует максимальному ветровому давлению – qmax=40даН/м2, максимальной скорости ветра – νmax=25м/с с повторяемостью 1 раз в 10 лет (ПУЭ РК 2003г., п.2.4.11., табл.2.5.1.);
Механические характеристики применяемого при расчете провода сведены в таблицу 11.1:
Таблица 11.1
| СИП-2AF | ||||||
| Число и номинальное сечение жил, штхмм2 | Диаметр несущей жилы d0, мм | Диаметр провода d, мм | Масса провода, кг/м | Разрывное усилие несущей жилы T, кН | Модуль упругости несущей жилы E, Н/мм2 | Коэффициент линейного расширения α, град–1 |
| 3x70+1x54.6 | 9.2 | 38 | 0.995 | 17 | 6250 | 23x10–6 |
| 3x95+1x70 | 9.85 | 41 | 1.307 | 21 | ||
| 3x120+1x95 | 12.2 | 49.3 | 1.608 | 30.4 | ||
| 3x150+1x95 | 52 | 1.881 | ||||
Расчетные климатические условия
При расчетах проводов ВЛИ на механическую прочность необходимо определять напряжения в проводах и стрелы провесов при всех возможных эксплуатационных сочетаниях климатических условий. Поскольку таких сочетаний может быть большое количество, то ПУЭ РК 2003г., п.2.5.33. устанавливают следующие расчетные сочетания климатических условий:
1) абсолютная максимальная температура воздуха (t+), ветер и гололед отсутствуют, удельная нагрузка от собственного веса провода – λ1 (режим высшей температуры);
2) абсолютная минимальная температура воздуха (t_), ветер и гололед отсутствуют, удельная нагрузка от собственного веса провода – λ1 (режим низшей температуры);
3) среднегодовая температура (tср), ветер и гололед отсутствуют, удельная нагрузка от собственного веса провода – λ1 (режим среднегодовой температуры);
4) температура воздуха –5°C, ветер отсутствует, провода покрыты гололедом, удельная нагрузка – λ3 (режим гололеда без ветра);
5) температура воздуха –5°C, максимальное ветровое давление, гололед отсутствует, удельная нагрузка – λ6 (ветровой режим);
6) температура воздуха –5°C, провода и тросы покрыты гололедом, ветровое давление q'=0.25·qmax, удельная нагрузка – λ7 (режим гололеда с ветром).
Расчет удельных нагрузок на провода
Провода ВЛИ испытывают действие нагрузок – вертикальных (вес провода и гололеда) и горизонтальных (давление ветра). В результате этих нагрузок в металле проводов возникают растягивающие напряжения. При расчетах на механическую прочность пользуются удельными нагрузками на провода. Под удельной нагрузкой понимают равномерно распределенную вдоль провода механическую нагрузку, отнесенную к единице длины и поперечного сечения. Удельные нагрузки выражаются в Ньютонах, отнесенных к 1м длины провода и к 1мм2 сечения: Н/(м·мм2).
Порядок определения удельных нагрузок
1. Удельная нагрузка от собственного веса провода – λ1:
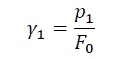
где p1 – вес одного метра провода, Н/м; F0 – фактическое сечение несущей жилы провода, мм2.
2. Удельная нагрузка от веса гололеда λ2 определяется исходя из условия, что гололедные отложения имеют цилиндрическую форму плотностью ρ0=9·10–3Н/(м·мм2):
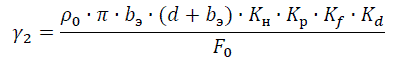
где bэ – толщина стенки гололеда, мм; d – диаметр провода, мм; F0 – фактическое сечение несущей жилы провода, мм2; Kн – коэффициент надежности по ответственности, принимаемый равным: 0.8 – для одноцепных ВЛИ до 1кВ; 1 – для двухцепных и многоцепных ВЛИ до 1кВ; Kр – региональный коэффициент, принимаемый равным 1 для ВЛИ до 1кВ; Kf – коэффициент надежности по гололедной нагрузке, равный 1.6 для районов по гололеду III и выше; Kd – коэффициент условий работы, равный 0.5.
3. Удельная нагрузка от собственного веса провода и веса гололеда – λ3:
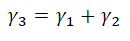
4. Удельная нагрузка от давления ветра, действующего перпендикулярно проводу при отсутствии гололеда – λ4:
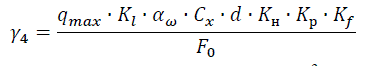
где qmax – максимальное ветровое давление, Н/м2; Kl – коэффициент, учитывающий влияние длины пролета на ветровую нагрузку, равный 1.2 при длине пролета до 50м; αω – коэффициент, учитывающий неравномерность ветрового давления по пролету ВЛ, принимаемый равным 0.85 при ветровом давлении 40даН/м2; Cx – коэффициент лобового столкновения, принимаемый равным 1.1 для СИП ВЛИ до 1кВ свободных или покрытых гололедом; d – диаметр провода, мм; Kн – коэффициент надежности по ответственности, принимаемый равным: 0.8 – для одноцепных ВЛИ до 1кВ; 1 – для двухцепных и многоцепных ВЛИ до 1кВ; Kр – региональный коэффициент, принимаемый равным 1 для ВЛИ до 1кВ; Kf – коэффициент надежности по ветровой нагрузке, равный 1.1; F0 – фактическое сечение несущей жилы провода, мм2.
5. Удельная нагрузка от давления ветра, действующего перпендикулярно проводу, при наличии гололеда – λ5:
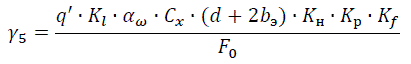
где q'=0.25·qmax; qmax – максимальное ветровое давление, Н/м2; Kl – коэффициент, учитывающий влияние длины пролета на ветровую нагрузку, равный 1.2 при длине пролета до 50м; αω – коэффициент, учитывающий неравномерность ветрового давления по пролету ВЛ, принимаемый равным 0.85 при ветровом давлении 40даН/м2; Cx – коэффициент лобового столкновения, принимаемый равным 1.1 для СИП ВЛИ до 1кВ свободных или покрытых гололедом; d – диаметр провода, мм; bэ – толщина стенки гололеда, мм; Kн – коэффициент надежности по ответственности, принимаемый равным: 0.8 – для одноцепных ВЛИ до 1кВ; 1 – для двухцепных и многоцепных ВЛИ до 1кВ; Kр – региональный коэффициент, принимаемый равным 1 для ВЛИ до 1кВ; Kf – коэффициент надежности по ветровой нагрузке, равный 1.1; F0 – фактическое сечение несущей жилы провода, мм2.
6. Удельная нагрузка от давления ветра и веса провода без гололеда – λ6:
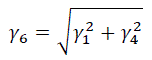
7. Удельная нагрузка от давления ветра и веса провода, покрытого гололедом – λ6:
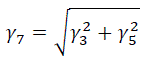
Удельные нагрузки для расчитываемых проводов сведены в таблицу 11.2:
Таблица 11.2
| Число и номинальное сечение жил, штхмм2 | λ1 | λ2 | λ3 | λ4 | λ5 | λ6 | λ7 |
| 3х70+1х54.6 | 0.147 | 0.271 | 0.418 | 0.283 | 0.126 | 0.319 | 0.437 |
| 3х95+1х70 | 0.168 | 0.316 | 0.484 | 0.266 | 0.115 | 0.315 | 0.497 |
| 3х120+1х95 | 0.135 | 0.187 | 0.322 | 0.208 | 0.084 | 0.248 | 0.333 |
| 3х150+1х95 | 0.158 | 0.195 | 0.353 | 0.22 | 0.087 | 0.271 | 0.405 |
Расчет провода на механическую прочность
Расчет проводов на механическую прочность ведется методом допустимых напряжений. Суть этого метода заключается в том, что напряжения в несущих жилах проводов в любом из эксплуатационных режимов не должны превышать допустимых напряжений. При выполнении этого условия материал несущей жилы провода работает в пределах упругих деформаций. Допустимые напряжения задаются ПУЭ в процентах от предела прочности несущей жилы провода (временного сопротивления несущей жилы провода).
Временное сопротивление несущей жилы провода σвр, Н/мм2, определяется делением разрывного усилия (предела прочности) несущей жилы провода на суммарное сечение несущей жилы:
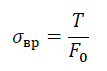
где T – разрывное усилие провода, Н (таблица 11.1); S – суммарное сечение несущей жилы провода, мм2.
Для обеспечения необходимой надежности в эксплуатации, несущие жилы проводов должны иметь определенный запас прочности, который при расчете принимается в зависимости от материала провода в процентах временного сопротивления разрыву при наибольшей внешней нагрузке σг, низшей температуре σ_ и при среднегодовой температуре σср.
Допускаемые напряжения для несущей жилы самонесущего изолированного провода при наибольшей нагрузке и низшей температуре – 40% от σвр, а при среднегодовой температуре – 30% от σвр.
Для рассчитываемых проводов значения временных сопротивлений несущих жил σвр и допустимые напряжения σг, σ_ и σср сведены в таблицу 11.3:
Таблица 11.3
| Число и номинальное сечение жил, штхмм2 | Временное сопротивление несущей жилы провода σвр, Н/мм2 | Допускаемое напряжение несущей жилы провода при наибольшей нагрузке и при низшей температуре σг= σ_, Н/мм2 | Допускаемое напряжение для несущей жилы провода при среднегодовой температуре σср, Н/мм2 |
| 3x70+1x54.6 | 256 | 102 | 76 |
| 3x95+1x70 | 276 | 110 | 82 |
| 3x120+1x95 | 260 | 104 | 78 |
| 3x150+1x95 |
Как видно из таблицы, допустимые напряжения при наибольшей нагрузке и наименьшей температуре принимаются больше соответствующих напряжений при среднегодовой температуре. Это обусловлено относительной кратковременностью первых двух режимов.
Важным этапом расчета проводов на механическую прочность является определение параметров исходного режима. В качестве такого режима можно принять любой режим, для которого известны удельная нагрузка, температура и напряжение. Однако при эксплуатации проводов напряжения в них не должны превышать соответствующих допустимых напряжений для режимов максимальной нагрузки, низшей и среднегодовой температур. Чтобы выполнить это условие, целесообразно при расчете в качестве исходного выбрать режим, в котором напряжение может достигать допустимого значения.
Для определения исходного режима используют так называемые критические пролеты. Суть понятия «критический пролет» заключается в следующем. На напряжение в несущей жиле провода оказывают влияние нагрузка и температура окружающей среды. Их влияние проявляется в большей или меньшей степени в зависимости от длины пролета. При малых пролетах на напряжение в несущей жиле провода значительное влияние оказывает температура, при больших пролетах – нагрузка. Граничный пролет, при котором влияние температуры и нагрузки на напряжения в проводе оказывается равноопасным, называется критическим.
Условия ограничения напряжения в несущей жиле провода в трех указанных выше режимах определяют три критических пролета.
Первый критический пролет lк1 – это пролет такой длины, при которой напряжение в несущей жиле провода в режиме среднегодовой температуры равно допустимому при среднегодовой температуре, а в режиме низшей температуры равно допустимому напряжению при низшей температуре.
Второй критический пролет lк2 – это пролет такой длины, при которой напряжение в несущей жиле провода при наибольшей нагрузке равно допустимому напряжению при наибольшей нагрузке, а в режиме низшей температуры равно допустимому напряжению при низшей температуре.
Третий критический пролет lк3 – это пролет такой длины, при которой напряжение в несущей жиле провода в режиме среднегодовой температуры равно допустимому при среднегодовой температуре, а в режиме наибольшей нагрузки равно допустимому напряжению при наибольшей нагрузке.
Общая формула для критических пролетов:
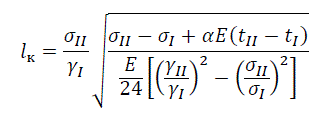
Подставив необходимые данные для рассчитываемых проводов, значения критических пролетов сводим в таблицу 5. За расчетный пролет примем lр=35м.
Для определения исходного режима по соотношению критических и расчетного пролетов воспользуемся таблицой 11.4:
Таблица 11.4
| Соотношение lк1, lк2, lк3 | Соотношение lр и lк | Параметры исходного режима |
| lк1<lк2<lк3 | lр<lк1 | σ_, λ1, t_ |
| lк1<lр<lк3 | σср, λ1, tср | |
| lр>lк3 | σг, λ7, tг | |
| lк1>lк2>lк3 | lр<lк2 | σ_, λ1, t_ |
| lр>lк2 | σг, λ7, tг | |
| lк1 – мнимый | lр<lк3 | σср, λ1, tср |
| lр>lк3 | σг, λ7, tг | |
| lк1 – мнимый, lк3<lк2 | lр>lк2 | σг, λ7, tг |
| lр<lк2 | σ_, λ1, t_ | |
| lк3 – мнимый, lк2<lк1 | lр>lк2 | σг, λ7, tг |
| lр<lк2 | σ_, λ1, t_ | |
| lк3 – мнимый | lр<lк1 | σ_, λ1, t_ |
| lр>lк1 | σср, λ1, tср | |
| lк1 и lк3 – мнимые | – | σср, λ1, tср |
Таблица 11.5
| Число и номинальное сечение жил, штхмм2 | lк1, м | lк2, м | lк3, м | Соотношение пролетов | Режим исходного состояния |
| 3x70+1x54.6 | мнимый | 35.9 | 79.41 | lр<lк3 | σср, λ1, tср |
| 3x95+1x70 | мнимый | 34.06 | 78.47 | lр<lк3 | σср, λ1, tср |
| 3x120+1x95 | мнимый | 49.48 | 117.28 | lр<lк3 | σср, λ1, tср |
| 3x150+1x95 | мнимый | 40.39 | 91.28 | lр<lк3 | σср, λ1, tср |
Основное уравнение состояния провода:
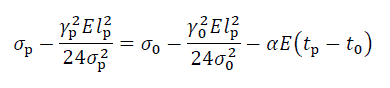
С помощью основного управления состояния провода можно найти напряжения в проводе в любых условиях работы воздушной линии на основании известных напряжений, нагрузок и температур в начальном состоянии.
Подставив необходимые данные для рассчитываемых проводов, значения механического напряжения при разных режимах и при разных выбранных пролетах сводим в таблицу 11.6:
Таблица 11.6
| СИП-2AF-3х70+1х54.6 | ||||||||
| Приведенная нагрузка λ, Н/м·мм2 | 0.437 | 0.418 | 0.147 | 0.147 | 0.319 | 0.147 | 0.319 | |
| Температура t, °C | –5 | –5 | –43 | 8.9 | 8.9 | 43 | 43 | |
| Гололед b, мм | 15 | 15 | 0 | 0 | 0 | 0 | 0 | |
| Ветер ν, м/с | 12.6 | 0 | 0 | 0 | 25 | 0 | 25 | |
| Пролет, м | Режим | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Тяжение, Н | ||||||||
| Напряжение σ, Н/мм2 | ||||||||
| Стрела провеса f, м | ||||||||
Расчетные данные таблицы 11.6 используются для проверки проводов на прочность, а также для расчета габаритов пересечений.
Выбор железобетонных стоек
Технические характеристики используемых железобетонных стоек приведены в таблице 11.7:
Таблица 11.7
| Марка стойки | Высота надземной части стойки, м | Ширина стойки, мм | Масса стойки, т | Расчетный изгибающий момент, кН·м |
| СВ95-1 | 7.1 | 165 | 0.75 | 14.7 |
| СВ95-2 | 7.1 | 165 | 0.75 | 19.6 |
| СВ95-3 | 7.1 | 165 | 0.9 | 29.4 |
| СВ105-3.5 | 8 | 190 | 1.2 | 34.3 |
| СВ105-3.6 | 8 | 190 | 1.2 | 35.3 |
| СВ105-5 | 8 | 190 | 1.2 | 49.1 |
| СВ110-3.5 | 8.5 | 165 | 1.1 | 34.3 |
| СВ110-5 | 8.5 | 165 | 1.1 | 49.1 |
Нормативная средняя составляющая нагрузки на опору, Н:

где Kw – коэффициент, учитывающий изменение ветрового давления по высоте в зависимости от типа местности; q – ветровое давление (см. исходные данные), Н/м2; Cx – коэффициент лобового сопротивления провода; A – площадь проекции, ограниченная контуром конструкции, ее части или элемента с наветренной стороны на плоскость перпендикулярно ветровому потоку, вычисленная по наружному габариту, м2.
Нормативная пульсационная составляющая ветровой нагрузки, Н:
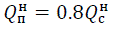
Расчетная ветровая нагрузка на конструкцию опоры, Н:
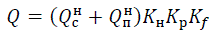
где Kн – коэффициент надежности по ответственности; Kр – региональный коэффициент; Kf – коэффициент надежности по ветровой нагрузке.
Расчетная линейная нагрузка от веса проводов с гололедом, воспринимаемая опорами, Н/м:
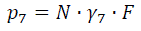
где N – количество проводов; λ7 – удельная нагрузка от давления ветра и веса провода, покрытого гололедом; F – суммарное сечение провода.
Расчетный суммарный горизонтальный (ветровой) момент, дейтсвувющий на абсолютно жесткую опору, Н·м:
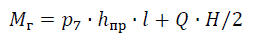
где hпр – высота подвески провода, м; l – длина пролета, м; H – высота надземной части опоры, м.
Расчетный суммарный вертикальный момент, дейтсвувющий на абсолютно жесткую опору:
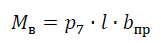
где bпр – расстояние от провода до оси опоры.
Расчетный суммарный изгибающий момент, действующий на абсолютно жесткую опору:
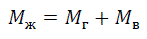
Равнодействующая горизонтальных сил:
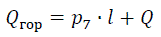
Высота точки приложения горизонтальных сил:
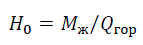
Прогиб в точке крепления проводов, м:
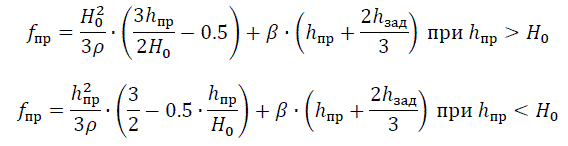
Прогиб в центре тяжести надземной части стойки опоры, м:
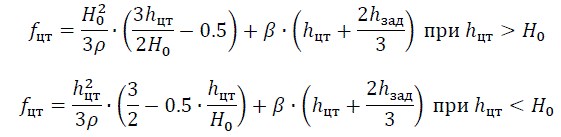
где 1/ρ – кривизна в опорном сечении (взято из книги по расчету мех. прочности опор для стоек СК), 1/ρ=0.0097 1/м; β – угол поворота стойки в заделке (β=0.01рад); hзад – глубина заделки стойки, м; hпт – высота центра тяжести стойки, м.
Расчетный суммарный изгибающий момент от вертикальных сил, Н·м:
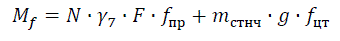
Суммарный изгибающий момент:
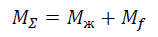
Результаты расчетов сводим в таблицу 11.8:
Таблица 11.8
| Стойка | Qсн, Н | Qпн, Н | Q, Н | p7, Н/м | Mг, Н·м | Mв, Н·м | Mж, Н·м | Qгор, Н | H0, м | fпр, м | fцт, м | Mf, Н·м | MΣ, Н·м |
| СИП-2AF-3х70+1х54.6 | |||||||||||||
| СВ95 | |||||||||||||
| СВ105 | |||||||||||||
| СВ110 | |||||||||||||
Суммарный изгибающий момент MΣ (таблица 11.8) не должен превышать расчетный изгибающий момент выбранной стойки (таблица 11.7). Снижение суммарного изгибающего момента достигается путем снижения расчетного пролета.
Источники:
1. Правила устройства электроустановок Республики Казахстан 2015г.
2. Правила устройства электроустановок Республики Казахстан 2008г.
3. Ответ Министра энергетики РК от 9 сентября 2019 года на вопрос от 28 августа 2019 года № 565120 (dialog.egov.kz).
4. А.П.Вихарев, А.В.Вычегжанин, Н.Г.Репкина. Проектирование механической части воздушных ЛЭП. Учебное пособие. - Киров, 2009.
5. Е.Н.Попов. Механическая часть воздушных линий электропередачи. Учебно-методическое пособие. - Благовещенск, 1998.
6. К.П.Крюков., Б.П.Новгородцев. Конструкции и механический расчет линий электропередачи. - Л: "Энергия", 1979.
7. П.И.Анастасиев., Ю.А.Фролов. Линии электропередачи до 10кВ промышленных предприятий. - М: "Энергия", 1980.
